Example of Continuity and Bernoulli's Equation.
BERNOULI'S EQUATION EXAMPLE
2)
A Venturimeter with an entrance diameter of 0.3m and a
throat diameter of 0.2m is used to measure the volume of gas flowing through a
pipe. The discharge coefficient of the meter is 0.96. Assuming the
specific weight of the gas to be constant at 19.62 N/m3, calculate
the volume flowing when the pressure difference between the entrance and the
throat is measured as 0.06m on a water U-tube manometer.
BERNOULI'S EQUATION EXAMPLE
Application of Bernoulli equation
1) In a
vertical pipe carrying water, pressure gauges are inserted at points A and B
where the pipe diameters are 0.15m and 0.075m respectively. The point B is 2.5m
below A and when the flow rate down the pipe is 0.02 cumecs, the pressure at B
is 14715N/m2 greater than that at A. Assuming the losses in the
pipe between A and B can be expressed as 
where v is the velocity at A, find
the value of k.
If the gauges at A and B are replaced by tubes filled with water and connected to a U-tube containing mercury of relative density 13.6, give a sketch showing how the levels in the two limbs of the U-tube differ and calculate the value of this difference in metres.
where v is the velocity at A, find
the value of k.If the gauges at A and B are replaced by tubes filled with water and connected to a U-tube containing mercury of relative density 13.6, give a sketch showing how the levels in the two limbs of the U-tube differ and calculate the value of this difference in metres.
Taking the datum at B, the Bernoulli equation becomes:
By continuity: Q = uAAA = uBAB
giving
Part ii)
What we know from the question:
Calculate Q.
For the manometer:
For the Venturimeter
Combining (1) and (2)
3)
A closed tank has an orifice 0.025m diameter in one of its
vertical sides. The tank contains oil to a depth of 0.61m above the centre of
the orifice and the pressure in the air space above the oil is maintained at
13780 N/m2 above atmospheric. Determine the discharge from the
orifice.
(Coefficient of discharge of the orifice is 0.61, relative density of oil is 0.9).
(Coefficient of discharge of the orifice is 0.61, relative density of oil is 0.9).
From the question
Apply Bernoulli,
Take atmospheric pressure as 0,
MOMENTUM EQUATION
EXAMPLE 1
What
force acts on the fireman’s nozzle of Example 1 assuming the inlet diameter is
60mm? The flow rate from the pump is 20 kg/s and the water jet velocity is 45
m/s.
M = ρA1v1
20 = 1000 x л/4 (60x 10-3)2
x v1
v1 = (4 x 20) / (1000 x л x (60
x 10-3)2
=
7.07 m/s (this is the force on the water)
mv1 = 20 x 45 = 900N
mv2 = 20 x 7.07 141.4 N
The force on the nozzle is equal and
opposite.
This is the force to be reacted by that
person holding the nozzle:
It is close to the average weight of
man (77kg)
EXAMPLE 2
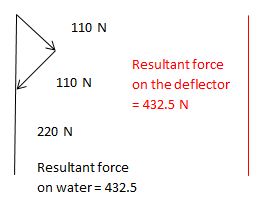
A water jet is directed on to a symmetrical deflector which splits
it in two and turns each stream through 165°. If the jet mass flow is 10 kg/s
and its velocity is 22 m/s what force is applied to the deflector? Assume the
jet is not slowed down by the deflector (i.e. frictionless flow)
mv1 = 22 x 10 = 220 N
mv2 = 22 x 5 = 110 N
mv3 = 22 x 5 = 110 N
Resultant force = mv2 + mv3 – mv1
 |
|||
 |
|||
kPa gage and leaves the whistle at atmospheric pressure through th Air enters the pipe at A at the rate of 6 kg /s under a pressure of 140 opening at B. The entering velocity of the air at A is 45 m/s, and theexhaust velocity at B is 360 m/s. Calculate the tension T, shear V, and bending moment M in the pipe at A. The net flow area at A is 7500 mm2.
BalasPadam